Kirchhoff's Current and Voltage Laws & circuit analysis sample

Kirchhoff's Current Law (KCL)
KCL states that the algebraic sum of
the currents in all the branches which
converge in a common node is equal
to zero
SI_in = SI_out
Kirchhoff's Voltage Law
Kirchhoff's Voltage Law states that the
algebraic sum of the voltages between
successive nodes in a closed path in
the network is equal to zero.
SE = SIR
Solution using Kirchhoff’s Voltage and
current laws
Steps to solve circuit by Kirchhoff’s
Laws.
1. Construct circuit with circuit magic
schematics editor.

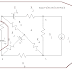
Circuit sample from circuit magic

2. Construct loops. (See “creating
loop” section in user guide) Number
of loops (and number of Kirhhoff’s
Voltage laws equations) can be
determined using following formula.
Loop can not include branches with
current sources. Due current sources
resistance equal infinity.
Loop Number = Branch Number –
(Nodes Number –1) – Current sources
Number
3. Select Analyze->Solve by Kirhhoff’s
laws menu item
4. In dialog box press OK button. if no
warning shown.
5. Read solution.
Solution example from circuit magic.
Writing Kirchhoff current law for 3-1
nodes
(Note number of Kirchhoff current
laws equations equal Nodes Number
–1)
(Node 1)J₁+I3+I₄+I7=0
(Node 2)-J₁ +I₂ -I₄=0
Wrining Kirchoff voltage law for 5-1-
(3-1) loops
(Loop1) I₃·R₃ -I₇ ·R₅ =-E₂
(Loop2) I₂ ·R₂ -I₇ ·R₅ +I₄ ·R₄ =E₁ -E₂
Linear equations
I₃+I₄ +I₇ =-2
I₂ -I₄ =2
10I₃ -10I₇ =-10
11I₂ +10I₄ -10I₇ =-7
Equations solution
I₁ =2
I₂ =0,692
I₃ =-0,846
I₄ =-1,308
I₇ =0,154